Concepts
This section explains the key concepts and conventions used in the DexRobot Kinematics library.
Coordinate Systems and Frames
The library uses two primary reference frames:
Hand Frame: Local coordinate system centered at the hand base.
Origin at the hand base/wrist
X-axis pointing toward palm
Y-axis pointing away from thumb for left hand, toward thumb for right hand
Z-axis pointing toward fingertips
World Frame: Global coordinate system. When using a hand in isolation:
The hand frame aligns with the world frame unless a base_pose is specified
With a base_pose, all computations transform between these frames
┌─────────┐ base_pose ┌──────────┐
│ World │ ───────────> │ Hand │
│ Frame │ <─────────── │ Frame │
└─────────┘ └──────────┘
The hand can be placed anywhere in the world frame by specifying a base_pose:
import numpy as np
import pinocchio as pin
from dexrobot_kinematics.utils.types import Position, Pose
# Create rotation matrix (90 degrees around Y axis)
R = pin.utils.rpyToMatrix(0, np.pi/2, 0)
# Create translation vector (1 meter in X direction)
t = np.array([1.0, 0.0, 0.0])
# Define base pose
base_pose = Pose(position=Position.from_array(t), orientation=R)
# Use in forward kinematics
poses = hand.forward_kinematics(joint_angles, base_pose=base_pose, frame="world")
The same base_pose can be used in inverse kinematics to transform target positions from the world frame to the hand frame.
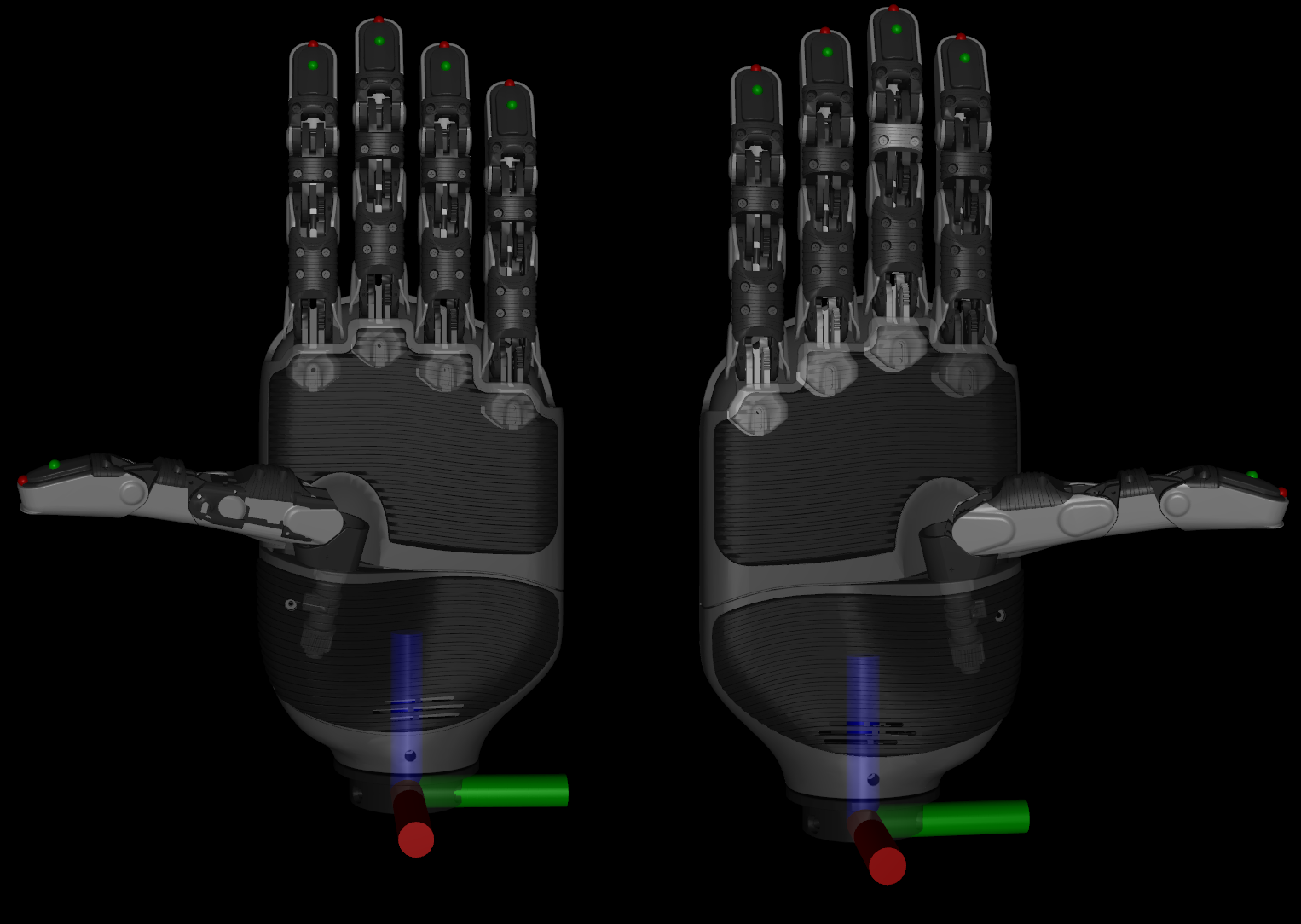
End Effector Types
The library supports two types of end effectors:
Fingerpads: The contact surfaces on each finger, used for grasping objects (green markers in the image below).
Fingertips: The very ends of each finger (red markers in the image below).

You can specify which end effector type to use in both forward and inverse kinematics:
# Get fingerpad poses
fingerpad_poses = hand.forward_kinematics(joint_angles, end_effector="fingerpad")
# Get fingertip poses
fingertip_poses = hand.forward_kinematics(joint_angles, end_effector="fingertip")
Inverse Kinematics Principles
The IK solver uses a damped least-squares method (Levenberg-Marquardt) to iteratively solve for joint angles:
Objective: Find joint angles that place end effector(s) at target position(s)
Method: - Start with initial guess for joint angles - Compute current end effector position - Calculate error vector (difference between current and target position) - Compute Jacobian matrix (relates joint velocities to end effector velocities) - Update joint angles using damped least-squares formula - Repeat until convergence or maximum iterations
The solver handles constraints including: - Joint limits - Joint coupling between PIP and DIP joints, consistent with the hand’s mechanical design